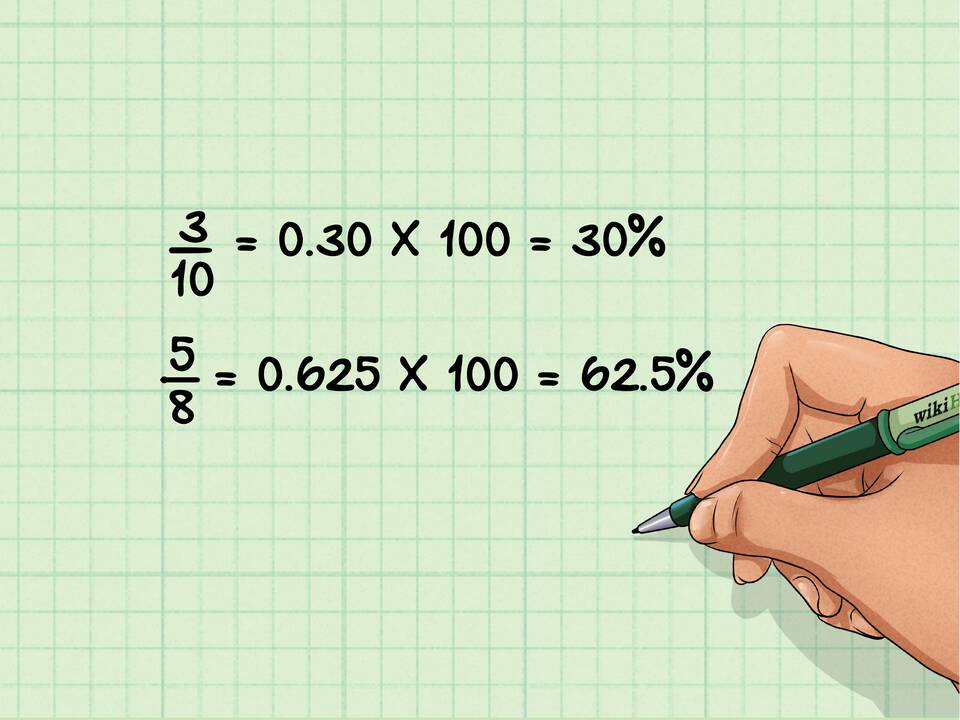Преобразование дробей в проценты - важный математический навык, необходимый в финансовых расчетах, статистике и повседневной жизни. Рассмотрим основные методы перевода.
Содержание
Преобразование дробей в проценты - важный математический навык, необходимый в финансовых расчетах, статистике и повседневной жизни. Рассмотрим основные методы перевода.
Основной метод преобразования
1. Перевод простых дробей
Для перевода обыкновенной дроби в проценты:
- Разделите числитель на знаменатель
- Умножьте результат на 100
- Добавьте знак процента (%)
| Дробь | Деление | Проценты |
| 1/2 | 1 ÷ 2 = 0,5 | 0,5 × 100 = 50% |
| 3/4 | 3 ÷ 4 = 0,75 | 0,75 × 100 = 75% |
Особые случаи
2. Перевод десятичных дробей
- 0,25 → 25% (умножить на 100)
- 1,5 → 150%
- 0,03 → 3%
3. Дроби с знаменателем 100
Если знаменатель равен 100, числитель сразу показывает процент:
- 17/100 = 17%
- 125/100 = 125%
Практическое применение
| Ситуация | Пример |
| Финансовые расчеты | 3/20 от суммы = 15% |
| Статистика | 7/10 респондентов = 70% |
| Скидки в магазине | 1/4 скидка = 25% |
Проверка правильности перевода
Чтобы убедиться в правильности преобразования:
- Процент всегда должен быть между 0% и 100% для правильных дробей
- Для неправильных дробей процент может превышать 100%
- Сумма процентов всех частей целого должна составлять 100%
Запоминающиеся примеры
- 1/1 = 100%
- 1/3 ≈ 33,33%
- 2/5 = 40%
- 5/8 = 62,5%
Освоив эти методы преобразования, вы сможете легко переводить любые дроби в проценты и применять эти знания в практических расчетах.
