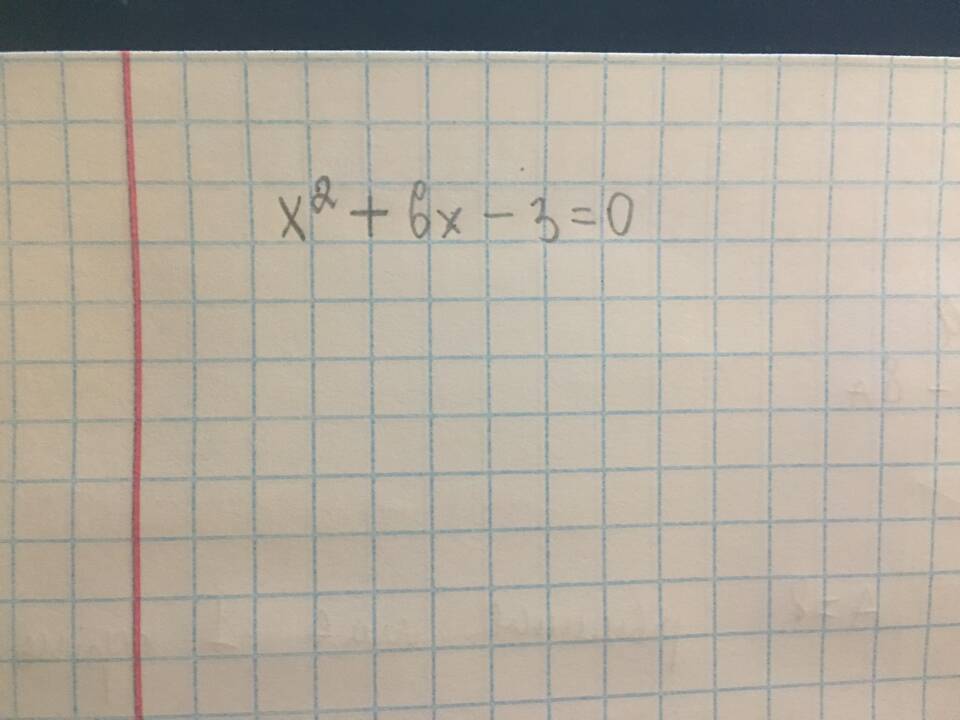Корень суммы двух или более чисел - это значение, получаемое при извлечении корня из результата сложения этих чисел. Математически это выражается формулой:
Содержание
Математическое определение
√(a + b + c + ...) = x, где x² = a + b + c + ...
Основные свойства корня суммы
- Корень суммы не равен сумме корней: √(a + b) ≠ √a + √b
- Для положительных чисел значение корня суммы всегда больше каждого из слагаемых в отдельности
- Корень суммы обладает свойством аддитивности только для определенных комбинаций чисел
Примеры вычислений
| Выражение | Результат |
| √(9 + 16) | 5 (так как 9+16=25, √25=5) |
| √(4 + 9 + 16) | 5.385 (так как 4+9+16=29, √29≈5.385) |
| √(1 + 1) | 1.414 (√2≈1.414) |
Особые случаи
Корень суммы квадратов
В геометрии часто встречается выражение √(a² + b²), которое представляет собой:
- Длину гипотенузы прямоугольного треугольника (теорема Пифагора)
- Модуль комплексного числа
- Норму вектора в двумерном пространстве
Приближенные вычисления
Для малых значений можно использовать приближение:
√(1 + x) ≈ 1 + x/2 - x²/8 + ... (при |x| < 1)
Практическое применение
- В геометрии для вычисления диагоналей и расстояний
- В физике при расчете результирующих векторов
- В статистике для вычисления среднеквадратичных отклонений
- В финансовой математике при оценке рисков
Ограничения и предостережения
При работе с корнями сумм важно учитывать:
- Область определения - подкоренное выражение должно быть неотрицательным
- Точность вычислений при работе с приближенными значениями
- Порядок операций при наличии других математических действий